This is part of a series of posts analysing the Chip-8 interpreter on the RCA COSMAC VIP computer. These posts may be useful if you are building a Chip-8 interpreter on another platform or if you have an interest in the operation of the COSMAC VIP. For other posts in the series refer to the index or instruction index.
INSTRUCTION GROUP: FX33
Convert VX to binary coded decimal (BCD) and store the result in the three bytes of memory pointed to by I
Binary Coded Decimal (BCD) is a means of storing decimal numbers in a binary format. There are two common methods for storing BCD numbers in an 8-bit system. The most efficient in terms of memory is to used packed BCD. With this encoding, each decimal digit occupies a nibble or four bits, so each byte holds two decimal digits. Chip-8 uses an uncompressed format, in which each digit is stored in a single byte. This might seem a strange choice given the efforts taken to save memory elsewhere in the interpreter. But to put it into context, for an 8-bit number, using an uncompressed rather than a packed BCD format makes the difference of just one byte, which is a good trade off against the additional complexity and length of a BCD routine to create a packed format. It also means the converted values can be loaded into VX and used directly with the FX29 instruction, which will point to the data for the relevant character sprite for that digit.
Only the least significant four bits of each byte are needed to hold each decimal digit, as shown in this table:
Binary value | Digit |
00000000 | 0 |
00000001 | 1 |
00000010 | 2 |
00000011 | 3 |
00000100 | 4 |
00000101 | 5 |
00000110 | 6 |
00000111 | 7 |
00001000 | 8 |
00001001 | 9 |
00001010 | Invalid value |
00001011 | Invalid value |
⋮ | Invalid values |
11111110 | Invalid value |
11111111 | Invalid value |
Chip-8 uses the division by digit value method to calculate the BCD digits. Here’s an example. Let’s say we were converting the binary value 01111011 (0x7B) into BCD. We are going to end up with three decimal digits from an 8-bit amount, since the maximum value is 255. So first we set these three digits to zero:
100s 10s 1s -------------- 0 0 0
Now we are going to calculate the a digit value for the 100s column. 100 in binary is 01100100 (0x64). First we try to subtract this from our original value:
01111011 01100100 - -------- 00010111 =
That worked so we can add one to the 100s column:
100s 10s 1s -------------- 1 0 0
The remainder from the previous operation (00010111) is now less than 100 (01100100) and a further subtraction would result in a negative value, so we know we are finished with the 100s column and 1 is the correct digit. Let’s move on to the 10s column. 10 in binary is 00001010 (0x0A). So we apply the same operation here – try to subtract this from the remainder of the previous operation:
00010111 00001010 - -------- 00001101 =
That worked, so we can add 1 to our 10s column:
100s 10s 1s -------------- 1 1 0
This time the remainder (0001101) is not less than 10 (0001010), so we repeat that operation:
00001101 00001010 - -------- 00000011 =
Once again we add 1 to our 10s column:
100s 10s 1s -------------- 1 2 0
At this point our remainder (00000011) is less than 10 (00001010) and a further subtraction would result in a negative value, so we know we are finished with the 10s column and 2 is the correct digit. So finally we move on to the 1s column. 1 in binary is 00000001 (0x01). Once again, we try to subtract this from the remainder of the previous operation:
00000011 00000001 - -------- 00000010 =
That worked, so we can add 1 to the 1s column:
100s 10s 1s -------------- 1 2 1
The remainder (00000010) is not less than 1 (00000001) so we repeat the operation:
00000010 00000001 - -------- 00000001 =
Once again we add 1 to our 1s column:
100s 10s 1s -------------- 1 2 2
The remainder (00000001) is not less than 1 (00000001) so we repeat the operation:
00000001 00000001 - -------- 00000000 =
Again, adding 1 to our 1s column:
100s 10s 1s -------------- 1 2 3
Now the remainder (00000000) is less than 1 (00000001) and a further subtraction would result in a negative number, so we know we are finished with our 1s column and 3 is the correct digit. And since there are no more columns to process we have our final decimal digits: 123.
Here’s that sequence, as it is implemented in the Chip-8 interpreter, shown as a flowchart:
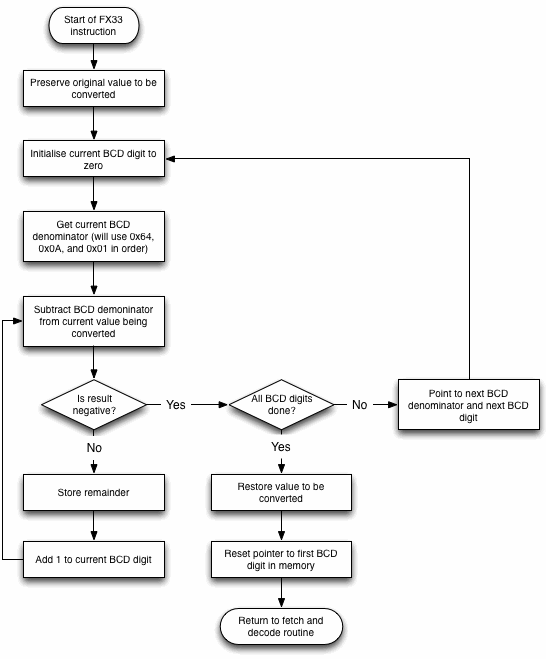
Here’s the interpreter code for this instruction:
Labels | Code (hex) | Comments |
BCD_ DENOMINATORS: | 64 0A 01 | Three constants with the decimal values of 100, 10 and 1, used by the BCD instruction FX33. |
011E – 0132 | The code for instructions FX1E and FX29 occupies this part of the interpreter. | |
FX33: | E6 | This is the entry point for instruction FX33. |
0134 | 06 | Get the value to be converted from VX. |
0135 | BF | Preserve the original value by temporarily storing it in RF.1. |
0136 | 93 | Get the high order byte of the address of the BCD denominator constants. |
0137 | BE | Store this in RE.1. |
0138 | F8 1B | Get the low order byte of the address of the BCD denominator constants. |
013A | AE | RE now points to first BCD denominator constant. |
013B | 2A | The I pointer (RA) is pointing to first byte of memory to store BCD but it needs to be moved to the byte before that before entering the loop. |
BCD_ LOOP: | 1A | Point I (RA) to location of next BCD digit. |
013D | F8 00 | Create a zero value. |
013F | 5A | Use this to initialise the BCD digit. |
DIVISION_ LOOP: | 0E | Get the current BCD constant. |
0141 | F5 | Subtract it from the current value of VX. |
0142 | 3B 4B | If the result is negative then the current digit is at the correct value, so move on to the next one. |
0144 | 56 | Store the remainder back in VX. |
0145 | 0A | Get the value of the current BCD digit. |
0146 | FC 01 | Add 1 to it. |
0148 | 5A | And put it back into memory. |
0149 | 30 40 | Continue to divide VX by current denominator. |
NEXT_DIGIT: | 4E | Get current BCD constant and point to next one. |
014C | F6 | Test the least significant bit |
014D | 3B 3C | If it’s not set (i.e. the constant we just used was not 0x01) then loop back and do the next digit. |
014F | 9F | Get the preserved original value of VX. |
0150 | 56 | Restore this to VX. |
0151 | 2A | This and the next instruction restores I (RA) so it is pointing to the first stored BCD digit. |
0152 | 2A |
|
0153 | D4 | Return to the fetch and decode routine. |
The execution time for this instruction is 80 machine cycles (363.2 microseconds) for the case of VX = 0. For each unit above zero in the 100s, 10s and 1s columns, add a further 16 machine cycles (72.64 microseconds). For example, if the converted number was 123, that would require 80 + (1 + 2 + 3) * 16 machine cycles, which is 176 machine cycles (799.04 microseconds). As this is a group FXXX instruction you will have to add the small overhead for the second stage decoding of these instructions. See this earlier post for details.
An obvious application for the BCD instruction is to convert a score, or other counter, before displaying it as a series of three character sprites (using instructions FX29 followed by DXY5. However, this instruction is limited in that it will only convert an 8-bit number, giving a range of 0 to 255.
This instruction should be handled by a contemporary Chip-8 interpreter. It’s not necessary to use this original algorithm as long as the outcome is the same.
Be First to Comment